
state - a dict holding current optimization state.Returns the state of the optimizer as a dict. Returns :Ī handle that can be used to remove the added hook by calling Hook ( Callable) – The user defined hook to be registered. Values are returned as a tuple containing the new_args and new_kwargs. IfĪrgs and kwargs are modified by the pre-hook, then the transformed The optimizer argument is the optimizer instance being used. Hook ( optimizer, args, kwargs ) -> None or modified args and kwargs Register an optimizer step post hook which will be called after optimizer step. Should be an object returnedįrom a call to state_dict().
Param_group ( dict) – Specifies what Tensors should be optimized along with group Trainable and added to the Optimizer as training progresses. This can be useful when fine tuning a pre-trained network as frozen layers can be made add_param_group ( param_group ) ¶Īdd a param group to the Optimizer s param_groups. This is in contrast to some otherįrameworks that initialize it to all zeros. Moreover, the initial value of the momentum buffer is set to the The Nesterov version is analogously modified. Input : γ (lr), θ 0 (params), f ( θ ) (objective), λ (weight decay), μ (momentum), τ (dampening), nesterov, maximize for t = 1 to … do g t ← ∇ θ f t ( θ t − 1 ) if λ ≠ 0 g t ← g t + λ θ t − 1 if μ ≠ 0 if t > 1 b t ← μ b t − 1 + ( 1 − τ ) g t else b t ← g t if nesterov g t ← g t + μ b t else g t ← b t if maximize θ t ← θ t − 1 + γ g t else θ t ← θ t − 1 − γ g t r e t u r n θ t \begin, \\
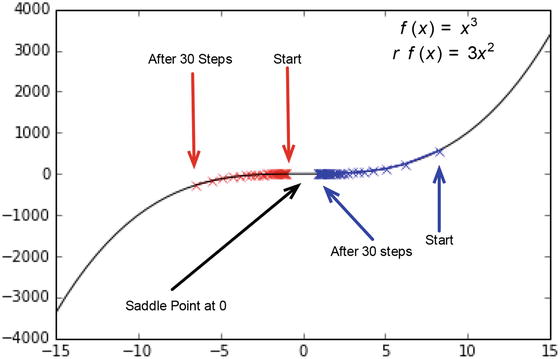
Extending torch.func with autograd.Function. CPU threading and TorchScript inference. CUDA Automatic Mixed Precision examples. Models are trained by using a large set of labeled data and neural network architectures that contain many layers. In deep learning, a computer model learns to perform classification tasks directly from images, text, or sound. Deep learning is a machine learning technique that teaches computers to do what comes naturally to humans. SGD, often referred to as the cornerstone for deep learning, is an algorithm for training a wide range of models in machine learning. Therefore, tuning such parameters is quite tricky and often costs days or even weeks before finding the best results. But learning overly specific with the training dataset could sometimes also expose the model to the risk of overfitting. In actual practice, more epochs can be utilized to run through the entire dataset enough times to ensure the best learning results based on the training dataset. This is just a simple demonstration of the SGD process. As a review, gradient descent seeks to minimize an objective function J ( θ ) ] =. SGD is a variation on gradient descent, also called batch gradient descent. Visualization of the gradient descent algorithm Stochastic gradient descent is being used in neural networks and decreases machine computation time while increasing complexity and performance for large-scale problems. Over the recent years, the data sizes have increased immensely such that current processing capabilities are not enough. The method seeks to determine the steepest descent and it reduces the number of iterations and the time taken to search large quantities of data points. The gradient descent continuously updates it incrementally when an error calculation is completed to improve convergence. In SGD, the user initializes the weights and the process updates the weight vector using one data point. The problem with gradient descent is that converging to a local minimum takes extensive time and determining a global minimum is not guaranteed. The gradient descent is a strategy that searches through a large or infinite hypothesis space whenever 1) there are hypotheses continuously being parameterized and 2) the errors are differentiable based on the parameters. Stochastic gradient descent (abbreviated as SGD) is an iterative method often used for machine learning, optimizing the gradient descent during each search once a random weight vector is picked. 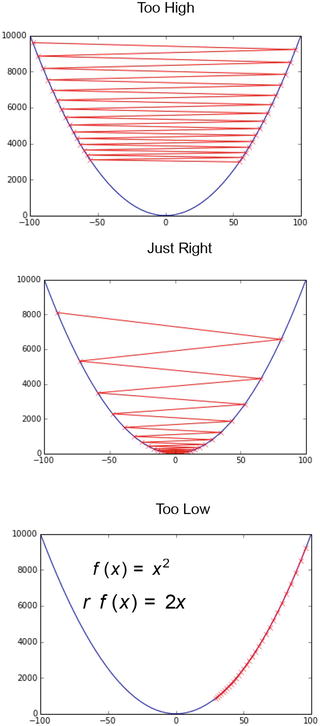
#STOCHASTIC GRADIENT DESCENT UPDATE#
3.5 Gradient Computation and Parameter Update.2.1 Stochastic Gradient Descent Algorithm.






 0 kommentar(er)
0 kommentar(er)
